- Excel для бухгалтера: исправление ошибки округления
- Абсолютная и относительная погрешности
- Вычислительные ошибки
- Вычислительные ошибки (ошибки округления)
- Добавление
- Доказательство
- Измерение ошибки округления с помощью машинного эпсилон
- Источники погрешностей
- Математическая модель задачи является неточной
- Машина эпсилон
- Накопление ошибки округления
- Нестабильные алгоритмы
- Нормализованная система с плавающей запятой
- Обозначение системы счисления с плавающей запятой
- Отображение формул
- Ошибка округления
- Ошибка округления при разных правилах округления
- Ошибка округления, вызванная арифметикой с плавающей запятой
- Ошибка представления
- Ошибки в исходных данных
- Пишем в excel слово истина или ложь как текст
- Плохо обусловленные проблемы
- Погрешность арифметических действий над приближенными числами
- Пример из реального мира: отказ ракеты patriot из-за увеличения ошибки округления
- Разделение
- Расчет ошибки округления в стандарте ieee
- Система счисления с плавающей запятой
- Стандарт ieee
- Субтрактивная отмена
- Теорема
- Умножение
Excel для бухгалтера: исправление ошибки округления
Бухгалтеры (и не только) знают «плохую» особенность Excel: обычно он позволяет неправильно складывать суммы. Это иногда приводит к неточностям в бухгалтерских документах, формируемых Excel (рис. 1)

Рис. 1. Инвойс с «неправильным» суммированием
Скачать заметку в формате Word, примеры из Excel
Мы видим, что общий налог (значение в ячейке G7) и стоимость товаров отличаются на один цент от суммы строк. Это ошибка округления. Но значение отображается только в формате с двумя десятичными знаками. В этих ячейках числовые значения больше десятичных (рис. 2) Excel складывает не отображаемые значения, а фактические значения.

Рис. 2. Тот же счет с большим количеством знаков после запятой.
Чтобы округлить значения в ячейках G4:G6, вы можете использовать формулу массива, чтобы округлить их до двух знаков после запятой перед их добавлением. [а]

Рис. 3. Исправьте сумму, используя формулу массива
Волшебная формула. Excel формирует виртуальный массив (в памяти компьютера), состоящий из трех элементов: OAROUND(G4;2), OOCRUGLER) и CONTENT. Так ! 🙂
Если вы хотите устранить ошибки округления, вы должны использовать функцию ОКРУГЛ в каждой ячейке диапазона G4:G6. Этот метод не требует формулы массива, но требует многократного повторения функции ОКРУГЛ. Вы имеете право судить, что легче!
[2] Идея взята из книги Джона Уокенбаха «MS Excel 2007» Библия пользователя. Если вы никогда не использовали таблицы, я рекомендую начать с заметки Excel. Знакомство с формулами массива.
Абсолютная и относительная погрешности
Точность результата расчета определяется погрешностью расчета. Ошибки бывают двух видов — абсолютные и относительные.
Абсолютная ошибка числа равна разнице между его истинным значением и приблизительным.
![]()
Где а — приблизительное значение числа х.
Относительная ошибка — это отношение между абсолютной точностью и приблизительным значением числа.
X вообще неизвестен. Существует только приблизительное значение а, и необходимо найти предельную ошибку х.
Вычислительные ошибки
Рассмотрим самые распространенные просчеты. Допустим, в исходных данных нет ошибок; однако, поскольку место в памяти компьютера зарезервировано для хранения чисел, точность представления чисел соответственно ограничена.
Вычислительные ошибки (ошибки округления)
Ошибки этого типа возникают из-за дискретной (а не непрерывной) формы представления величин в ЭВМ. Благодаря расчетам можно избежать ошибок.
Добавление
Автоматическое сложение состоит из выравнивания десятичных знаков двух добавляемых чисел, их сложения и сохранения результата в виде числа с плавающей запятой. Сложение может быть выполнено с большей точностью, но результат должен быть округлен до указанной точности.
Например, при добавлении к двойной точности IEEE следующим образом ,
1{ displaystyle 1}2-53{ displaystyle 2 ^ {- 53}}1,00…0×20 1,00…0×2-53знак равно1.00…0⏟52 бит×20 0.00…0⏟52 бит1×20знак равно1.00…0⏟52 бит1×20{ displaystyle { begin {align} 1,00 ldots 0 times 2 ^ {0} 1,00 ldots 0 times 2 ^ {- 53} & = 1. underbrace {00 ldots 0} _ { text { 52 бита}} times 2 ^ {0} 0. Underbrace {00 ldots 0} _ { text {52 бит}} 1 times 2 ^ {0} & = 1. underbrace {00 ldots 0} _ { text {52 бита}} 1 times 2 ^ {0} end {выровнено}}}
Из этого примера видно, что при сложении большого числа и малого числа может возникнуть ошибка округления, поскольку сдвиг десятичных знаков в мантиссах для согласования показателей степени может вызвать потерю некоторых цифр.
Доказательство
Пусть где , и пусть будет представление с плавающей запятой . Поскольку используется пошаговое определение, это означает:
* Чтобы определить максимум этого количества, необходимо найти максимум числителя и минимум знаменателя. Поскольку (нормализованная система), минимальное значение знаменателя равно . Сверху числитель ограничен . Таким образом, . Поэтому для пошаговой инструкции. Доказательство для округления до ближайшего аналогично.
Иксзнак равноd0.d1d2…dп-1dп…×βп∈р{ displaystyle x = d_ {0} .d_ {1} d_ {2} ldots d_ {p-1} d_ {p} ldots times beta ^ {n} in mathbb {R}}п∈[L,U]{ Displaystyle п в [L, U]}жл(Икс){ displaystyle fl (x)}Икс{ displaystyle x}|Икс-жл(Икс)||Икс|знак равно|d0.d1d2…dп-1dпdп 1…×βп-d0.d1d2…dп-1×βп||d0.d1d2…×βп|знак равно|dп.dп 1…×βп-п||d0.d1d2…×βп|знак равно|dп.dп 1dп 2…||d0.d1d2…|×β-п{ displaystyle { begin {align} { frac {| x-fl (x) |} {| x |}} & = { frac {| d_ {0} .d_ {1} d_ {2} ldots d_ {p-1} d_ {p} d_ {p 1} ldots times beta ^ {n} -d_ {0} .d_ {1} d_ {2} ldots d_ {p-1} times beta ^ {n} |} {| d_ {0} .d_ {1} d_ {2} ldots times beta ^ {n} |}} & = { frac {| d_ {p}. d_ {p 1} ldots times beta ^ {np} |} {| d_ {0} .d_ {1} d_ {2} ldots times beta ^ {n} |}} & = { frac {| d_ {p} .d_ {p 1} d_ {p 2} ldots |} {| d_ {0} .d_ {1} d_ {2} ldots |}} times beta ^ {- p} end {выровнено}}}d0≠0{ displaystyle d_ {0} neq 0}1{ displaystyle 1}(β-1).(β-1)(β-1)¯знак равноβ{ Displaystyle ( бета -1). ( бета -1) { overline {( бета -1)}} = бета}|Икс-жл(Икс)||Икс|≤β1×β-пзнак равноβ1-п{ displaystyle { frac {| x-fl (x) |} {| x |}} leq { frac { beta} {1}} times beta ^ {- p} = beta ^ {1 -п}}ϵзнак равноβ1-п{ displaystyle epsilon = beta ^ {1-p}}
- Обратите внимание, что первое определение эпсилон-машины не совсем эквивалентно второму определению при использовании правила округления до ближайшего, но оно эквивалентно для последовательного перехода.
Измерение ошибки округления с помощью машинного эпсилон
Машинный эпсилон может использоваться для измерения уровня ошибки округления при использовании двух вышеупомянутых правил округления. Ниже приведены формулы и соответствующие доказательства. Здесь используется первое определение машинного эпсилон.
ϵмаcчас{ displaystyle epsilon _ {mach}}
Источники погрешностей
Попробуем выявить причины ошибок.
Математическая модель задачи является неточной
Ошибка связана с тем, что сам численный метод или математическая модель являются аппроксимацией точного алгоритма (например, дифференцирования). Но любая модель или математический метод могут вносить существенные ошибки, если не учитывать некоторые особенности задачи.
Шаблон может быть совершенно неприемлемым при определенных условиях. Эта ошибка называется методологической. Он все еще существует, даже при совершенно точных данных и совершенно точных расчетах. В большинстве случаев погрешность численного метода можно уменьшить, изменив параметры метода (например, уменьшив шаг выборки или увеличив число итераций).
Машина эпсилон
Машинный эпсилон может использоваться для измерения уровня ошибки округления в системе счисления с плавающей запятой. Вот два разных определения.
- ϵмаcчасзнак равноМаксимумИкс|Икс-жл(Икс)||Икс|{ displaystyle epsilon _ {mach} = max _ {x} { frac {| x-fl (x) |} {| x |}}}
Накопление ошибки округления
Ошибки могут накапливаться, когда последовательность вычислений применяется к началу входного представления с ошибкой округления.
Нестабильные алгоритмы
Говорят, что алгоритм или числовой процесс стабилен, если во входных данных происходят лишь небольшие изменения.
Последовательность вычислений обычно происходит при запуске какого-либо алгоритма. Количество ошибок в результате зависит от стабильности алгоритма . Ошибка округления будет увеличиваться из-за нестабильных алгоритмов.
Например, для с данным. Это легко показать . Предположим, что это наше начальное значение и есть небольшая ошибка представления , что означает, что начальный вход в этот алгоритм вместо . Затем алгоритм выполняет следующую последовательность вычислений.
упзнак равно∫01ИкспИкс 5dИкс{ displaystyle y_ {n} = int _ {0} ^ {1} , { frac {x ^ {n}} {x 5}} dx}пзнак равно1,2,…,8{ Displaystyle п = 1,2, ldots, 8}у0{ displaystyle y_ {0}}упзнак равно1п-5уп-1{ displaystyle y_ {n} = { frac {1} {n}} — 5лет_ {n-1}}у0{ displaystyle y_ {0}}ϵ{ displaystyle epsilon}у0 ϵ{ displaystyle y_ {0} epsilon}у0{ displaystyle y_ {0}}
- у1знак равно1-5(у0 ϵ)знак равно1-5у0-5ϵу2знак равно12-5(1-5у0-5ϵ)знак равно12-5 25у0 52ϵ⋮упзнак равно… 5пϵ{ displaystyle { begin {align} y_ {1} & = 1-5 (y_ {0} epsilon) = 1-5y_ {0} -5 epsilon y_ {2} & = { frac { 1} {2}} — 5 (1-5y_ {0} -5 epsilon) = { frac {1} {2}} — 5 25y_ {0} 5 ^ {2} epsilon vdots y_ {n} & = ldots 5 ^ {n} epsilon end {выровнено}}}
Ошибка округления увеличивается при последующих вычислениях, поэтому алгоритм не стабилен.
Нормализованная система с плавающей запятой
- Система счисления с плавающей запятой нормализуется, если первая цифра всегда отлична от нуля, если только число не равно нулю. Поскольку мантисса равна , мантисса ненулевого числа в нормализованной системе удовлетворяет . Таким образом, нормализованная форма ненулевого числа с плавающей запятой IEEE — это где . В двоичном формате ведущая цифра всегда отображается, поэтому она не записывается и называется неявным битом. Это дает дополнительный бит точности, так что ошибка округления, вызванная ошибкой представления, уменьшается.d0{ displaystyle d_ {0}}d0.d1d2…dп-1{ displaystyle d_ {0} .d_ {1} d_ {2} ldots d_ {p-1}}1≤ мантисса <β{ displaystyle 1 leq { text {мантисса}} < beta}±1.бб…б×2E{ displaystyle pm 1.bb ldots b times 2 ^ {E}}б∈0,1{ displaystyle b in {0,1}}1{ displaystyle 1}
- Поскольку система счисления с плавающей запятой конечна и дискретна, она не может представлять все действительные числа, что означает, что бесконечные действительные числа могут быть аппроксимированы только некоторыми конечными числами с помощью правил округления . С плавающей точкой приближения заданного вещественного числа В можно обозначить.
F{ displaystyle F}Икс{ displaystyle x}жл(Икс){ displaystyle fl (x)}- Общее количество нормализованных чисел с плавающей запятой равно
- 2(β-1)βп-1(U-L 1) 1{ Displaystyle 2 ( бета -1) бета ^ {p-1} (U-L 1) 1}, куда
- 2{ displaystyle 2} считает выбор знака, положительный или отрицательный
- (β-1){ Displaystyle ( бета -1)} считает выбор первой цифры
- βп-1{ displaystyle beta ^ {p-1}} считает оставшуюся мантиссу
- U-L 1{ Displaystyle U-L 1} считает выбор показателей
- 1{ displaystyle 1}считает тот случай, когда число есть .0{ displaystyle 0}
- 2(β-1)βп-1(U-L 1) 1{ Displaystyle 2 ( бета -1) бета ^ {p-1} (U-L 1) 1}, куда
Обозначение системы счисления с плавающей запятой
Система счисления с плавающей запятой характеризуется целыми числами:
F{ displaystyle F}4{ displaystyle 4}
- β{ displaystyle beta}: основание или основание
- п{ displaystyle p}: точность
- [L,U]{ displaystyle [L, U]}: диапазон экспоненты, где — нижняя граница, а — верхняя границаL{ displaystyle L}U{ displaystyle U}
- Иксзнак равно±(d0.d1d2…dп-1⏟мантисса)β×βE⏞экспонентазнак равно±d0×βE d1×βE-1 … dп-1×βE-(п-1){ displaystyle x = pm ( underbrace {d_ {0} .d_ {1} d_ {2} ldots d_ {p-1}} _ { text {mantissa}}) _ { beta} times beta ^ { overbrace {E} ^ { text {exponent}}} = pm d_ {0} times beta ^ {E} d_ {1} times beta ^ {E-1} ldots d_ {p-1} times beta ^ {E- (p-1)}}
- где — такое целое число, что для , и — такое целое число, что .dя{ displaystyle d_ {i}}0≤dя≤β-1{ displaystyle 0 leq d_ {i} leq beta -1}язнак равно0,1,…,п-1{ Displaystyle я = 0,1, ldots, п-1}E{ displaystyle E}L≤E≤U{ Displaystyle L leq E leq U}
Отображение формул
Заполните данными ячейки, так как показано ниже на рисунке:
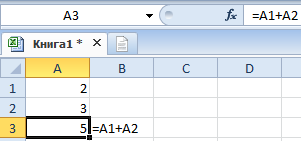
Как правило, комбинация символов в B3 считается формулой, и расчет выполняется автоматически. Но что, если мы не хотим вычислять результат? Другой способ решения проблемы описан выше.
Ошибка округления
Давным-давно, в советское время, я читал знаменитую повесть Артура Кларка. Читать в советском стиле. Критический нуль был широко распространен в СССР. Это когда рецензент сам увидел «Звездные войны» и рассказал нам, насколько это отвратительно. Так и здесь — кто-нибудь из советских мастеров, вроде Казанцева или другого. Прочитал рассказ «Стена» — потом стал его ругать за безыдейность. Безыдейность была настолько безобразна, что рассказ, даже в коротком рассказе, вызывал удивление и восхищение. По мере того, как история оживала и менялась, я придумал альтернативные концовки.
Я расскажу историю.
Множество удивительных миров, плывущих по Реке Времени. Другие, очень немногие, идут против течения; еще меньше тех, кто находится за его пределами и не знает ни будущего, ни прошлого. Маленькая вселенная Шервана не была одной из них. Он состоял из одного мира — планеты племени Шерван и одной звезды Трилорн.
(c) перевод имени Лев Львович Жданов
В мире, находящемся ниже уровня развития середины позапрошлого века и достигшем зрелости в середине прошлого века, есть стена. Казалось бы, непреодолимая высокая преграда в виде высокой горы. Стена была простой – всегда. Продолжая кругосветное путешествие, она разделила его на две половины: мир света и мир тьмы. Планета, на которой разворачиваются события и происходит действие, постоянно обращена к местному светилу одной стороной — примерно как лунная луна)
Главный герой, местный аристократ Шерван, хочет узнать, что находится за стеной. Он тратит много денег, чтобы построить огромную кирпичную лестницу. У стены, доходящей почти до самого верха — охраняемый Шерван боится того ужаса, который таится за стеной. Ну или хочет быть первым — и принимает меры, чтобы любопытный работник не опередил его.
Вот предлагаю вам перечитать рассказ «Темная стена» (1949), который есть в сети.
В тот день Шерван взбирается на вершину стены и видит расстилающуюся вдалеке темную равнину.
Он смело идет во тьме и через несколько страшных мгновений видит во тьме светящееся отражение. Он устремляется к свету, который вспыхивает и становится ярче. Шерван видит солнце, горы и горные вершины — за стеной мир, идентичный или похожий на этот другой.
А чуть дальше он осознает страшную истину: мир за стеной не похож на мир вокруг — вот и все! Он видит лестницу, построенную его людьми!
Шерван был создан как лента Мёбиуса, у которой есть только одна сторона!
Это такая замечательная история. Со многими интересными подробностями — например, цивилизация мира Шерван находится в упадке — когда-то строили ажурные мосты над ущельями и стальные корабли, способные плавать в зоне вечного полудня (помните, что цивилизация этого мира существует на узкой полосе окружающий мир? чем выше солнце над горизонтом, тем жарче)
Откуда они? Шерван не помнит «дней гнева» — и дома, уцелевшие от старых домов, целы. Я предполагаю, что они просто покинули маленькую вселенную Шервана — создав миры по своему вкусу *
* В закрытой цивилизации без звездного света и без будущего цивилизация — единственная цивилизация. Они постараются не отправиться в другую вселенную, а создать ее для себя. Итак, Шерван, если бы я хотел продолжить эту историю дальше, я нашел проходы в иные миры — созданные волей древних и населенные потомками их предков.
P S. Теперь, перечитав рассказ еще раз — я заметил, что мне будет ясно — за стеной ничего нет. Просто потому, что холодная сторона планеты высосала влагу из воздуха и превратилась в лед! Через некоторое время вода на холодной стороне окажется вся в воде, а если этого не произошло, значит, за стеной ничего нет.
А запомнилась мне эта история потому, что в детстве я нашел массу вариантов того, с чем Шерван столкнулся за стеной — начиная с простых, вроде того, что за стеной находится ледяная цивилизация на основе аммиака, и заканчивая комплексами, в которых Вернувшийся Шерван обнаруживает, что мир, в который он вернулся, — не его собственный, а просто похожий.
Но лестница взорвалась, и Шерван, сомневавшийся в реальности, имел основания считать себя сумасшедшим.
Пер Гюнт не в состоянии описать, что с ним происходит. Он встречает гения уровня Леонардо да Винчи и получает удовольствие; Альтернативный путь, по которому Шерван сбегает из этого мира и находит свою копию в другом мире.
Что вы думаете о том, что нашел Шерван, когда взобрался на стену?
Ошибка округления при разных правилах округления
Существует два общих правила округления: на один шаг и на одно ближе. Стандарт IEEE использует округление до ближайшего.
- Поочередно : расширение по основанию усекается после цифры.
β{ displaystyle beta}Икс{ displaystyle x}(п-1)тчас{ Displaystyle (п-1) ^ {th}}- Это правило округления необъективно, потому что оно всегда приближает результат к нулю.
- Округление до ближайшего : устанавливается до ближайшего числа с плавающей запятой . При равенстве используется число с плавающей запятой, последняя сохраненная цифра которого четная.
жл(Икс){ displaystyle fl (x)}Икс{ displaystyle x}- Для стандарта IEEE, где основание равно , это означает, что при наличии ссылки она округляется до последней цифры .β{ displaystyle beta}2{ displaystyle 2}0{ displaystyle 0}
- Это правило округления является более точным, но требует больших вычислительных ресурсов.
- Округление таким образом, чтобы последняя сохраненная цифра была четной, если она равна, гарантирует, что она не будет систематически округляться в большую или меньшую сторону. Это сделано для того, чтобы избежать возможности нежелательного медленного изменения в длинных вычислениях просто из-за смещения округления.
- В следующем примере показан уровень ошибки округления в соответствии с двумя правилами округления. Правило округления, округление до ближайшего, в целом приводит к меньшей ошибке округления.
| Икс | По очереди | Ошибка округления | Округление до ближайшего | Ошибка округления |
|---|---|---|---|---|
| 1,649 | 1.6 | 0,049 | 1.6 | 0,049 |
| 1,650 | 1.6 | 0,050 | 1,7 | 0,050 |
| 1,651 | 1.6 | 0,051 | 1,7 | -0,049 |
| 1,699 | 1.6 | 0,099 | 1,7 | -0,001 |
| 1,749 | 1,7 | 0,049 | 1,7 | 0,049 |
| 1,750 | 1,7 | 0,050 | 1,8 | -0,050 |
Ошибка округления, вызванная арифметикой с плавающей запятой
Несмотря на то, что некоторые числа могут быть точно представлены именами машин, и эти числа называются машинами, выполнение этих операций может привести к ошибке округления в конечном результате.
Ошибка представления
Ошибка, которая возникает, когда вы пытаетесь представить число, используя конечную строку цифр в качестве ошибки округления, называется ошибкой представления. Есть ошибки в десятичных представлениях, но их можно исправить.
| Обозначение | Представление | Приближение | Ошибка |
|---|---|---|---|
| 1/7 | 0. 142 857 | 0,142 857 | 0,000 000 142 857 |
| пер 2 | 0,693 147 180 559 945 309 41 … | 0,693 147 | 0,000 000 180 559 945 309 41 … |
| журнал 10 2 | 0,301 029 995 663 981 195 21 … | 0,3010 | 0,000 029 995 663 981 195 21 … |
| 3 √ 2 | 1,259 921 049 894 873 164 76 … | 1,25992 | 0,000 001 049 894 873 164 76 … |
| √ 2 | 1,414 213 562 373 095 048 80 … | 1,41421 | 0,000 003 562 373 095 048 80 … |
| е | 2,718 281 828 459 045 235 36 … | 2,718 281 828 459 045 | 0,000 000 000 000 000 235 36 … |
| π | 3,141 592 653 589 793 238 46 … | 3,141 592 653 589 793 | 0,000 000 000 000 000 238 46 … |
Увеличение количества цифр, разрешенных в представлении, уменьшает количество возможных ошибок округления. Но любое представление с ограниченным конечным числом факторов вызовет некоторую степень ошибки округления для неисчислимого количества действительных чисел. Дополнительные цифры, используемые на промежуточных этапах вычислений, называются сторожевыми цифрами.
Многократное округление приводит к накоплению ошибок. Если 9,945309 округлить до двух знаков после запятой (9,95), то будет считаться один (10) в меньшую сторону. тогда общая ошибка равна 0,054691. 9,945309 округляется до одного десятичного знака за один шаг. Обычно это происходит при выполнении арифметических операций (см. Underflow).
Ошибки в исходных данных
Во входных данных задачи входные данные часто являются основным источником ошибок. Такие ошибки неизбежны и возникают во всех реальных задачах, потому что любое измерение возможно только с предельной точностью. Вместе с ошибками, вносимыми математической моделью, и фатальной ошибкой при решении задачи они называются совершенно невозможными ошибками.
Необходимо стремиться к тому, чтобы все исходные данные были примерно равными. Сильное уточнение исходных данных не приводит к повышению точности конечных результатов. Если измерения неверны, их можно исключить.
Пишем в excel слово истина или ложь как текст
Есть два способа заставить программу обрабатывать слова логических типов данных как текст:
- Сначала введите символ формата.
- Изменяет формат ячейки на текст.
В ячейках А1 и А2 реализуем первый способ, а во второй — второй.
Задача 1. В ячейку A1 введите слово с символом форматирования, например: «истина». Обязательно в начале слова ставьте символ апострофа «‘», который можно вводить из английской раскладки (не в русской). Когда Excel скрывает первый символ, он обрабатывает слова «истина» как текст.
Задача 2. Найдите ячейку A2 и вызовите диалоговое окно «Формат ячеек». Как вызвать контекстное меню правой кнопкой мыши. В списке числовых форматов выберите «текст» и нажмите «ОК».
Задание 3. Для сравнения напишите это же слово в ячейке А3 без апострофа и изменения формата.
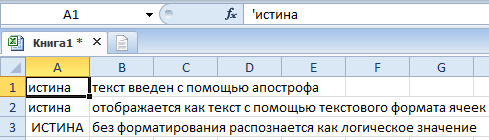
Как видите, апостроф виден только в строке формул.
Отметить. В ячейках А1 и А2 текстовые символы не заменены большими символами, так как слово воспринимается программой как слово.
Плохо обусловленные проблемы
Даже если используется стабильный алгоритм, решение проблемы может быть неточным из-за накопления ошибок округления, когда сама проблема плохо обусловлена .
Число обусловленности проблемы — это отношение относительного изменения решения к относительному изменению входных данных. Проблема хорошо обусловлена, если небольшие относительные изменения входных данных приводят к небольшим относительным изменениям в решении. В противном случае проблема плохо обусловлена . Другими словами, проблема является плохо обусловленной, если ее число условий «намного больше», чем .
1{ displaystyle 1}
Номер условия вводится для обозначения ошибок округления, которые могут возникнуть при решении некорректных задач.
Погрешность арифметических действий над приближенными числами
Если вы выполняете операции над приблизительными числами, вы можете оценить предельную погрешность результата. При умножении или делении чисел их относительные ошибки складываются:
![]()
![]()
При возведении приближенного числа в степень его относительная ошибка увеличивается в степени.
![]()
При сложении или вычитании чисел их абсолютные погрешности складываются:
Относительная ошибка суммы положительных членов рассчитывается следующим образом:
![]()
Отсюда следует, что относительная погрешность суммы нескольких чисел одного знака лежит между большей относительной точностью слагаемых:
![]()
![]()
При сложении ошибка будет сильно зависеть от абсолютных значений добавляемых чисел. Рассмотрим пример сложения двух чисел, одинаковых по модулю:
1234 0.005678 = 1234.00005678
или в компьютерном представлении:
1.234Е 03 5.678Е-03 = 1.234005678Е 03
После сложения количество значащих цифр равно 10. С точностью (float) число содержит всего 8 цифр, то есть фактически равно 1,2340056E 03. При сложении пропали две цифры. Из-за этого потеря точности здесь происходит от того, что при сложении с большим количеством малых чисел результат сложения выходит за пределы точности.
Теперь рассмотрим сложение чисел разных знаков, или их вычитание. Согласно выражению (П.7), относительная ошибка может быть очень большой, если числа близки друг к другу
Таким образом, сложение и вычисление являются неустойчивыми операторами: для некоторых данных даже небольшая ошибка в исходных данных может вызвать большую разницу в результатах. Погрешность можно уменьшить правильной последовательностью операций.
Пример из реального мира: отказ ракеты patriot из-за увеличения ошибки округления

Соединенные Штаты построили ракету Patriot.
25 февраля 1991 года во время войны в Персидском заливе батарея американских ракет Patriot не смогла перехватить иракскую баллистическую ракету Scuda. В США скад врезался в казармы американской армии. В отчете Главного бухгалтерского управления под названием «Patriot Missile Defense: проблема с программным обеспечением, вызвавшая сбой системы в Дахране, Саудовская Аравия» указана причина сбоя: неточное время от запуска из-за компьютерных арифметических ошибок. В частности, время в десятых долях секунды было умножено на 10, чтобы получить расстояние в секунду. Этот расчет был выполнен с использованием 24-битного регистра без фиксированной точки. Цифра 1/10 была разбита через 24 бита после точки счисления. Небольшая ошибка прерывания, умноженная на большое число в десятых долях секунды, чтобы получить время 10 секунд, приводила к значительной ошибке. Правильно, батарея Патриота продержалась почти 100 часов, а время отключения составило около 0,34 секунды. (Число 1/10 равно. Это означает, что двоичное расширение 1/10 равно. Патриот теперь хранит 24-битный регистр вместо того, чтобы принимать двоичную или грубую десятичную ошибку. Умножение на количество десятых долей секунды в часах дает сумму из цифр «10» и «12». Скад проходит примерно 1/24 1/25 1/28 1/29 1/212 1/213 …{ displaystyle 1/2 ^ {4} 1/2 ^ {5 } 1 /2 ^ {8} 1/2 ^ {9} 1/2 ^ {12} 1/2 ^ {13} ldots} 0,000110011001100110011001100100… {displayStyle 0.00011001100110011001100110000} 0,0001100000011001100110000 {displaystyle 0100100000000000000000000000000000000 {affichestyle 0100000000000000000000000000100000000 {Displaystyle 010000000000000000000000000000000000 { DisplayStyle 0100000000000000000000000000000010000001000000001000000000000 {affichage … {DisplayStyle 0,000000000000000000000000011001100 LDOTS} 0 .000000095 {DisplayStyle 0,000000095} 100 {DisplayStyle 100} 0,000000095 × 100 × 60 × 60 × 10 = 0,34 {DisplayStyle 0, 000000095 times 100 times 60 умножить на 10 = 0,34} 1 676 МЕТРОВ, что больше, чем h на данный момент проходит полтора километра. Патриот сделал это для того, чтобы приближающийся Скад оказался за пределами «дальнобойных ворот», за которыми следовал его Па. трио. По иронии судьбы, тот факт, что просчет времени был улучшен не во всех частях кода и все еще мог сохранять ошибки.
Разделение
Как правило, частное мантисс-цифр может содержать больше, чем -цифров. Таким образом, в результат будет включена ошибка округления.
2{ displaystyle 2}п{ displaystyle p}п{ displaystyle p}
- Например, если приведенная выше нормализованная система с плавающей запятой все еще используется, то, но . Итак, хвост отрезается. fl(0,333 ldot) = 3,3 x 10^{-1}}0,333…-3,3×10-1 = 0,00333…{displaystyle 0,333 ldot -3,3 x 10^{-1} = 0, 00333 ldot}
Расчет ошибки округления в стандарте ieee
Предположим, что применяется округление до ближайшего значения и двойная точность IEE.
- 1.0010110011001100110011001100110011001100110011001100⏟52 бит110…×23{ displaystyle 1. underbrace {0010110011001100110011001100110011001100110011001100} _ { text {52 бит}} 110 ldots times 2 ^ {3}}
Поскольку бит справа от двоичной точки — это a, за которым следуют другие ненулевые биты, правило округления до ближайшего требует округления в большую сторону , то есть добавления бита к биту. Таким образом, нормализованное представление с плавающей запятой в стандарте IEEE является
53рd{ displaystyle 53 ^ {rd}}1{ displaystyle 1}1{ displaystyle 1}52пd{ displaystyle 52 ^ {nd}}9,4{ displaystyle 9.4}
- жл(9,4)знак равно1.0010110011001100110011001100110011001100110011001101×23{ displaystyle fl (9.4) = 1,0010110011001100110011001100110011001100110011001101 times 2 ^ {3}}.
Это представление получается отбрасыванием бесконечного хвоста
- 0.1100¯×2-52×23знак равно0.0110¯×2-51×23знак равно0,4×2-48{ displaystyle 0. { overline {1100}} times 2 ^ {- 52} times 2 ^ {3} = 0. { overline {0110}} times 2 ^ {- 51} times 2 ^ { 3} = 0,4 times 2 ^ {- 48}}
от правого хвоста, а затем добавили на этапе округления.
1×2-52×23знак равно2-49{ displaystyle 1 times 2 ^ {- 52} times 2 ^ {3} = 2 ^ {- 49}}
- Тогда .жл(9,4)знак равно9,4-0,4×2-48 2-49знак равно9,4 (0,2)10×2-49{ displaystyle fl (9,4) = 9,4–0,4 times 2 ^ {- 48} 2 ^ {- 49} = 9,4 (0,2) _ {10} times 2 ^ {- 49}}
- Таким образом, ошибка округления равна .(0,2×2-49)10{ displaystyle (0,2 times 2 ^ {- 49}) _ {10}}
Система счисления с плавающей запятой
По сравнению с системой счисления с фиксированной запятой, система счисления с плавающей запятой более эффективна при представлении действительных чисел, поэтому она широко используется в современных компьютерах. В то время как действительные числа бесконечны и непрерывны, система счисления с плавающей запятой конечна и дискретна. Таким образом, ошибка представления, которая приводит к ошибке округления, возникает в системе счисления с плавающей запятой.
р{ Displaystyle mathbb {R}}F{ displaystyle F}
Стандарт ieee
В стандарте IEEE база бинарная, т. Е. Используется нормализация. Стандарт IEEE хранит знак, показатель степени и мантиссу в отдельных полях слова с плавающей запятой, каждое из которых имеет фиксированную ширину (количество бит). Два наиболее часто используемых уровня точности для чисел с плавающей запятой — это одинарная точность и двойная точность.
βзнак равно2{ displaystyle beta = 2}
| Точность | Знак (биты) | Экспонента (биты) | Мантисса (биты) |
|---|---|---|---|
| Одинокий | 1 | 8 | 23 |
| Двойной | 1 | 11 | 52 |
Субтрактивная отмена
Вычитание двух почти равных чисел называется вычитанием .
- Когда начальные цифры отменены, результат может быть слишком маленьким для точного представления, и он будет представлен только как .
0{ displaystyle 0} - Даже при несколько большем значении результат в типичных случаях все равно существенно ненадежен. Нет особой веры в точность значения, потому что наибольшая неопределенность в любом числе с плавающей запятой — это цифры в крайнем правом углу.
ϵ{ displaystyle epsilon}
Теорема
- По очереди: ϵмаcчасзнак равноβ1-п{ displaystyle epsilon _ {mach} = beta ^ {1-p}}
- Округление до ближайшего: ϵмаcчасзнак равно12β1-п{ displaystyle epsilon _ {mach} = { frac {1} {2}} beta ^ {1-p}}
Умножение
В общем, произведение мантисс- цифр содержит до цифр, поэтому результат может не соответствовать мантиссе. Таким образом, в результат будет включена ошибка округления.
2{ displaystyle 2}п{ displaystyle p}2п{ displaystyle 2p}
- Например, рассмотрим нормализованную систему счисления с плавающей запятой, в которой цифры основания и мантиссы не превышают . тогда и . Внимание, а так там только цифры мантиссы. Ошибка округления будет следующей }}2{ стиль отображения 2}6776-fl(6776)=6776-6,7×103=76{ стиль отображения 6776-fl(6776)=6776-6,7 умножить на 10^ {3}=76}





![{ Displaystyle п в [L, U]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ce9241edd62373f0714b77a6670e4abfc9c0d96)































![{ displaystyle [L, U]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41ec87812b949abde24429affe0606f2fc2b9809)



























